|
Поиск Лекций
Использование критерия NPV теоретически обоснованно, и в целом он считается наиболее корректным измерителем эффективности инвестиций. Вместе с тем применение абсолютных показателей при анализе проектов с различными исходными условиями (первоначальными инвестициями, сроками экономической жизни и др.) может приводить к затруднениям при принятии управленческих решений. Пример 2.3 Предположим, что рассматриваются два проекта. Принятая норма дисконта составляет 10%. Соответствующие оценки денежных потоков и расчет NPV приведены в табл. 2.3. Т а б 1 и ц а 2.3. Условия реализации проектов (пример 2.3)
Чистая современная стоимость обоих проектов составляет 5000 и в случае необходимости выбора не позволяет однозначно определить лучший вариант. Поэтому наряду с абсолютным показателем эффективности инвестиций NPV используются также и относительные — индекс рентабельности и внутренняя норма доходности.
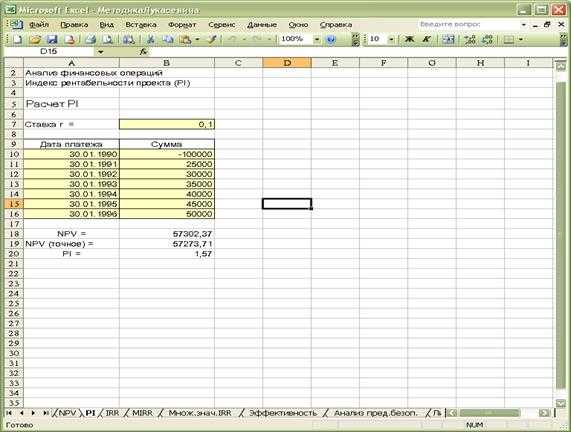
Индекс рентабельности (benefit-cost ratio, profitability index — РГ) показывает, сколько единиц современной величины денежного потока приходится на единицу предполагаемых первоначальных затрат. Для расчета этого показателя используется следующая формула Если величина критерия PI > 1, то современная стоимость денежного потока проекта превышает первоначальные инвестиции, обеспечивая тем самым наличие положительной величины NPV. При этом норма рентабельности превышает заданную, и проект следует принять. При PI = 1 величина NPV = О, и инвестиции не приносят дохода. Если PI<1, проект не обеспечивает заданного уровня рентабельности и его следует отклонить. Общее правило PI: если Р1> 1, то проект принимается, иначе — его следует отклонить. На Листе5 введите данные таблицы 2.3 и рассчитайте индексы рентабельности для примера 2.3 согласно формулам:. Р1Х= 15000/ 10000= 1,50; Ply = 105 000 /100 000 = 1,05. Переименуйте Листе5 в PI. Таким образом, проект X обеспечивает большую рентабельность инвестиций и в случае невозможности реализации обоих проектов ему следует отдать предпочтение. Несмотря на то, что в ППП EXCEL нет специальной функции для вычисления индекса рентабельности, определить его можно довольно легко, например, делением ячейки, содержащей функцию расчета NPV, на ячейку, содержащую величину первоначальных инвестиций, и последующим прибавлением к результату единицы. Рассчитаем индекс рентабельности для примера 2.1. Для этого в ячейке В20 листа NPV сформированной ранее таблицы задайте одну из следующих формул (рис. 2.6): -B18 / В10 + 1 (Результат: 1,57) -B19 / В610 + 1 (Результат: 1,57). Знак минус в формуле необходим для получения положительного результата, так значение ячейки В6 (первоначальные инвестиции) — отрицательная величина. Сохраните полученную таблицу на магнитном диске.
Рис. 2.6. Расчет индекса рентабельности Применение показателя PI часто бывает полезным в случае, когда существует возможность финансирования нескольких проектов, но при этом инвестиционный бюджет фирмы ограничен. Пример 2.4 Фирма рассматривает возможность участия в финансировании шести проектов, предполагаемые условия реализации которых приведены в табл. 2 4. Инвестиционный бюджет фирмы равен 250 000 ден.ед. Перейдите на Лист6 и переименуйте его в Проекты A-F. Создайте шаблон таблицы 2.4. Таблица 2.4. Условия реализации проектов для примера 2.4
Для расчета NPV=PV‑I введите в соответствующие ячейки формулы. Также введите формулы для расчета PI=PV/I в соответствующие ячейки. Результаты сравните с таблицей 2.4.1. Таблица 2.4.1 Условия реализации проектов для примера 2.4
Как видим по данным табл. 2.4.1, все проекты имеют положительную NPV и, если бы инвестиционный бюджет фирмы не был ограничен суммой в 250 000 ден.ед., их следовало бы принять. Однако в силу ограниченности бюджета может быть реализован только тот набор (портфель) проектов, при котором суммарные инвестиции не превышают 250 000 ден.ед. В данном случае существует несколько таких портфелей, поэтому возникает проблема выбора наиболее эффективной комбинации проектов. В условиях ограниченного бюджета наиболее эффективен (оптимален) для фирмы такой портфель проектов, который обеспечивает наибольшую отдачу вложенных средств и в конечном результате генерирует максимальную NPV. Оптимальный портфель инвестиций в подобных условиях можно получить путем последовательного включения проектов в порядке убывания индексов рентабельности и проверки соблюдения ограничений. Расположим проекты, приведенные в табл. 2.4, в порядке убывания индексов рентабельности (выполните сортировку данных по убыванию значений в поле PI). Добавьте столбец и рассчитайте NPV нарастающим итогом. Результаты представлены в таблице 2.5.
Та блица 2.5. Классификация проектов по индексам рентабельности
Как видим по данным из табл. 2.5, оптимальный в этих условиях портфель инвестиций будет состоять из проектов С, D и В. При этом суммарная NPV портфеля равна: NPV =NPV(C) + NPV(D) + NPV(B) = 106 000,00 ден.ед. Более эффективное решение подобных проблем может быть получено при использовании методов математического программирования и рассмотрено ниже. Индекс рентабельности не всегда обеспечивает однозначную оценку эффективности инвестиций, и проект с наиболее высоким PI может • не соответствовать проекту с наиболее высокой NPV. В частности, использование индекса рентабельности может привести к ошибочным результатам при оценке взаимоисключающих проектов. Рассмотрим следующий пример. Пример 2.5 Фирма рассматривает возможность участия в финансировании двух взаимоисключающих проектов, предполагаемые условия реализации которых приведены в табл. 2.6. Принятая норма дисконта для проектов одинакова и равна 10%. Необходимо выбрать наиболее эффективный проект инвестиций. На Листе7 сделайте расчеты как показано в таблице 2.6. Таблица 2.6. Потоки платежей проектов (пример 2.5)
Определим индексы рентабельности для проектов 1 и 2: PI1 = 388,43 / 100,00 = 3,88; Р12 = 34 927,52 / 10 000,00 = 3,43. Нетрудно заметить, что при наличии у фирмы соответствующих средств второй проект предпочтительнее, так как он генерирует большую NPV. Однако индекс рентабельности «отдает» предпочтение первому проекту. Обычно расчет индекса рентабельности дополняет расчет NPV с целью отбора проектов, порождающих максимальную современную стоимость на единицу затрат.
Рекомендуемые страницы: Поиск по сайту |
|
poisk-ru.ru
Индекс доходности проекта (PI)
•«=ВСД(CF0:CFn;i)». Функция включена по умолчанию. Как видите, она не учитывает даты выплат, в формуле предполагается, что выплаты происходят с одной и той же периодичностью. i здесь — это предполагаемое значение ставки, которая нужна для облегчения процедуры расчёта IRR в случае расчётов больших потоков платежей. Получаемая по этой формуле ставка соответствует промежуткам времени, между членами потока. То есть, если у нас ежемесячные выплаты, то и IRR получится месячной. В английском офисе функция называется по-другому — «irr»;
•«=ЧИСТВНДОХ(CF0:CFn;t0:tn;i)». Для включения формулы требуется подключить надстройку «Пакет анализа». i здесь — также предполагаемое значение ставки. В этой формуле уже учитываются даты и в результате расчётов получается более точная годовая ставка. В английском офисе функция называется «xirr»;
PI (Profitability Index) – это индекс, который можно рассматривать как вариант оценки рентабельности проекта в дисконтированной форме. Этот индекс представляет собой отношение приведённых доходов к приведённым расходам:
|
|
| ∑ | CFk+ |
|
|
|
|
PI = CF | + |
| t k−t | 0 |
| |||
| 100%= | k | 1 i |
|
| 100% , | (4.4.15) | |
|
| CFn– |
|
| ||||
CF – |
| ∑ |
|
|
|
| ||
|
|
| t n−t | 0 |
| |||
|
|
| n | 1 i |
|
|
|
|
Индекс доходности выступает некоторым аналогом NPV. Так, если у нас приведённые доходы совпадают с приведёнными расходами, то индекс равен 100%. Индекс доходности больше 100% соответствует NPV > 0, а индекс меньший 100% — отрицательной величине
NPV.
Срок окупаемости проекта (DPP)
Срок окупаемости (DPP, DPBP, DPB, PBP — «Discounted PayBack Period») определяется суммированием последовательных членов ряда доходов, дисконтированных по ставке i, до тех пор, пока не будет получена сумма, равная объёму первоначальных инвестиций. То есть, фактически, пока не будет получен NPV = 0. Показатель применим в случае, если наша инвестиционная схема подразумевает разовую первоначальную инвестицию с периодическими положительными членами потока после неё. В MS Excel данный показатель можно рассчитать через функцию «Поиск решения».
Модифицированная внутренняя норма доходности MIRR (Modified IRR)
Чуть ранее, рассказывая про IRR мы заметили, что при непосредственном подборе его значения, всего может быть найдено m ставок (где m соответствует количеству периодов платежей). Кроме того, в IRR подразумевает, что поток инвестиций и поток доходов учитываются по одной и той же процентной ставке. Однако логично предполагать, что поток инвестиций должен быть реинвестирован по одной ставке, а поток доходов — по другой.
Эти два недостатка были исправлены в модифицированной внутренней норме доходности. Расчёт её осуществляется следующим образом.
studfiles.net
Рассчитать показатели эффективности инвестиционных проектов (npv,irr,pi,dpp(срок окупаемости).
Рассчитаем показатели эффективности для первого проекта.
0 | 1 | 2 | 3 | 4 | 5 | |
Инвестиции | 12 500 |
|
|
|
|
|
Выручка |
| 40 000 | 45 000 | 45 000 | 45 000 | 45 000 |
Переменные затраты |
| -20 800 | -23 400 | -23 400 | -23 400 | -23 400 |
Условно-постоянные затраты |
| -17 000 | -17 000 | -17 000 | -17 000 | -17 000 |
Амортизация |
| 1 750 | 1 750 | 1 750 | 1 750 | 1 750 |
Балансовая прибыль |
| 2 200 | 4 600 | 4 600 | 4 600 | 4 600 |
Налог на прибыль |
| -440 | -920 | -920 | -920 | -920 |
Чистая прибыль |
| 1 760 | 3 680 | 3 680 | 3 680 | 3 680 |
Сальдо по операционной деятельности |
| 3 510 | 5 430 | 5 430 | 5 430 | 5 430 |
Дисконтированное сальдо по опер.деят-ти |
| 2 968 | 3 883 | 3 284 | 2 777 | 2 349 |
Текущая стоимость доходов рассчитывается по формуле
И для первого проекта NPVравна (2968+3883+3284+2777+2349)-12500=2761.
Внутренняя норма доходности определяется как
И для первого проекта IRR=0,27+(0,275-0,27)∙12/(12+121)=27,05%.
Рентабельность активов
Дисконтированный срок окупаемости инвестиций
DPP=3+2364/2777=3,85 года.
Рассчитаем показатели эффективности для второго проекта.
0 | 1 | 2 | 3 | 4 | 5 | |
Инвестиции | 22 900 |
|
|
|
|
|
Выручка |
| 35 000 | 37 500 | 37 500 | 35 000 | 0 |
Переменные затраты |
| -19 320 | -20 700 | -20 700 | -19 320 | 0 |
Условно-постоянные затраты |
| -6 900 | -6 900 | -6 900 | -6 900 | -6 900 |
Амортизация |
| 3 206 | 3 206 | 3 206 | 3 206 | 3 206 |
Балансовая прибыль |
| 8 780 | 9 900 | 9 900 | 8 780 | -6 900 |
Налог на прибыль |
| -1 756 | -1 980 | -1 980 | -1 756 | 1 380 |
Чистая прибыль |
| 7 024 | 7 920 | 7 920 | 7 024 | -5 520 |
Сальдо по опер.деят-ти |
| 10 230 | 11 126 | 11 126 | 10 230 | -2 314 |
Дисконтированное сальдо по опер.деят-ти |
| 8 651 | 7 957 | 6 729 | 5 232 | -1 001 |
NPV=4668;
PI=1,2;
IRR=28,86%;
DPP=2,93.
Рассчитаем показатели эффективности для третьего проекта.
0 | 1 | 2 | 3 | 4 | 5 | |
Инвестиции | 18 600 |
|
|
|
|
|
Выручка |
| 26 250 | 31 500 | 31 500 | 31 500 | 31 500 |
Переменные затраты |
| -10 250 | -12 300 | -12 300 | -12 300 | -12 300 |
Условно-постоянные затраты |
| -11 000 | -11 000 | -11 000 | -11 000 | -11 000 |
Амортизация |
| 2 232 | 2 232 | 2 232 | 2 232 | 2 232 |
Балансовая прибыль |
| 5 000 | 8 200 | 8 200 | 8 200 | 8 200 |
Налог на прибыль |
| -1 000 | -1 640 | -1 640 | -1 640 | -1 640 |
Чистая прибыль |
| 4 000 | 6 560 | 6 560 | 6 560 | 6 560 |
Сальдо по опер.деят-ти |
| 6 232 | 8 792 | 8 792 | 8 792 | 8 792 |
Дисконтированное сальдо по опер.деят-ти |
| 5 270 | 6 288 | 5 317 | 4 497 | 3 803 |
NPV=6574;
PI=1,35;
IRR=32,22%;
DPP=3,32.
studfiles.net
NPV формула расчета пример. NPV инвестиционного проекта
Инвестировать — это значит вложить свободные финансовые ресурсы сегодня с целью получения стабильных денежных потоков в будущем. Вкладываться можно в финансовые инструменты, или в новый бизнес, или в расширение уже существующего бизнеса. В любом случае, инвестирование — это вложение денег в какие-то активы на долгосрочную перспективу.
Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
Для этого можно воспользоваться одним из методов оценки эффективности инвестиционных проектов. NPV — это один из таких методов. Найти NPV инвестиционного проекта означает найти чистую приведенную стоимость всех денежных потоков, связанных с этим проектом.
Как это сделать, используя формулу для расчета NPV, и так ли это сложно, читайте ниже.
Что можно делать с деньгами?
Если у вас появилась некоторая сумма денег, то есть три возможности ими распорядиться:
- а) потратить — купить большую квартиру и жить в ней, купить автомобиль и ездить на нем на работу, съездить в отпуск на Гавайи. У каждого есть свои варианты, ведь, чтобы потратить деньги, советчики не нужны.
- б) спрятать в сейф на «черный день». И всё время трястись, что их украдут. И с грустью наблюдать, как они обесцениваются в результате инфляции
- в) «вложить» (инвестировать) куда-нибудь с целью получения дохода в будущем. А будет ли это выгодно?
Эта статья для тех, кто выбирает третий пункт из этого списка. И не важно, собираетесь ли вы инвестировать свои деньги или деньги компании, в которой вы будете работать финансовым специалистом.

Инвестировать можно в банк, положив деньги на депозит, а можно купить долговые обязательства или акции банков или компаний, которые свободно торгуются на финансовом рынке. Это самый простой путь, но не самый доходный. Для физических лиц, то есть нас с вами, чаще всего, это единственный способ вложения накоплений.
А можно инвестировать в бизнес, что означает купить долгосрочные активы (основные средства), используя которые в процессе производства, торговли или оказания услуг, вы будете получать в будущем притоки денежных средств. Для юридических лиц (компаний) это собственно говоря, и является целью их существования — делать деньги (прибыль) из инвестиций.
Чтобы определить, будет ли успешным тот или иной инвестиционный проект, финансовыми специалистами используются определенные методы оценки проектов. Два основных метода — это NPV и IRR.
NPV — что это такое? Какая логика в этом показателе?
NPV — это сокращение по первым буквам фразы «Net Present Value» и расшифровывается это как чистая приведенная (к сегодняшнему дню) стоимость. Это метод оценки инвестиционных проектов, основанный на методологии дисконтирования денежных потоков.
Если вы знаете перспективный бизнес-проект и хотите вложить в него деньги, то неплохо было бы для начала рассчитать NPV (=чистую приведенную стоимость) этого бизнес-проекта. Алгоритм расчета такой:
- 1) нужно оценить денежные потоки от проекта — первоначальное вложение (отток) денежных средств и ожидаемые поступления (притоки) денежных средств в будущем
- 2) определить стоимость капитала (cost of capital) для вас — это будет ставкой дисконтирования
- 3) продисконтировать все денежные потоки (притоки и оттоки) от проекта по ставке, которую вы оценили в п.2)
- 4) Сложить. Сумма всех дисконтированных потоков и будет равна NPV проекта
Правило: если NPV больше нуля, то проект можно принять, если NPV меньше нуля, то проект стоит отвергнуть.
Логическое обоснование метода NPV очень простое. Если NPV равно нулю, это означает, что денежные потоки от проекта достаточны, чтобы
- а) возместить инвестированный капитал и
- б) обеспечить необходимый доход на этот капитал.
Если NPV положительный, значит, проект принесет прибыль, и чем больше величина NPV, тем выгоднее/прибыльнее является данный проект. Поскольку доход кредиторов (у кого вы брали деньги в долг) фиксирован, весь доход выше этого уровня принадлежит акционерам. Если компания одобрит проект с нулевым NPV, позиция акционеров останется неизменной – компания станет больше, но цена акции не вырастет. Однако, если проект имеет положительную NPV, акционеры станут богаче.
Формула NPV — пример расчета
Формула расчета NPV выглядит сложно на взгляд человека, не относящего себя к математикам:
Где:
- n, t — количество временных периодов,
- CF — денежный поток (Cash Flow),
- R — стоимость капитала (ставка дисконтирования, Rate)
На самом деле эта формула — всего лишь правильное математическое представление суммирования нескольких величин. Чтобы рассчитать NPV, возьмем для примера два проекта А и Б, которые имеют следующую структуру денежных потоков в ближайшие 4 года:
Оба проекта А и Б имеют одинаковые первоначальные инвестиции в 10,000, но денежные потоки в последующие годы сильно разнятся. Проект А предполагает более быструю отдачу от инвестиций, но к четвертому году денежные поступления от проекта сильно упадут. Проект Б, напротив, в первые два года показывает более низкие денежные притоки, чем поступления от Проекта А, но зато в последующие два года Проект Б принесет больше денежных средств, чем проект А.
Рассчитаем NPV инвестиционного проекта следующим образом:
Предположения для упрощения расчета:
- а) все денежные потоки случаются в конце каждого года,
- б) первоначальный денежный отток (вложение денег) произошел в момент времени «ноль», т.е. сейчас
- б) стоимость капитала (ставка дисконтирования) составляет 10%
Про дисконтирование денежных потоков на этом сайте есть отдельная статья. Если расчет, приведенный ниже, вам покажется совсем непонятным, то лучше будет сначала вспомнить основы дисконтирования, вернувшись к этой статье.
Коротко напомню: чтобы привести денежный поток к сегодняшнему дню, нужно умножить денежную сумму на коэффициент 1/(1+R), при этом (1+R) надо возвести в степень, равную количеству лет. Величина этой дроби называется фактором или коэффициентом дисконтирования. Чтобы не вычислять каждый раз этот коэффициент, его можно посмотреть в специальной таблице, которая называется «таблица коэффициентов дисконтирования».
Применим формулу NPV для Проекта А. У нас четыре годовых периода и пять денежных потоков. Первый поток (10,000) — это наша инвестиция в момент времени «ноль», то есть сегодня. Если развернуть формулу NPV, приведенную чуть выше, то мы получим сумму из пяти слагаемых:
Если подставить в эту сумму данные из таблицы для Проекта А вместо CF и ставку 10% вместо R, то получим следующее выражение:
То, что стоит в делителе, можно рассчитать, но проще взять готовое значение из таблицы коэффициентов дисконтирования и умножить эти коэффициенты на сумму денежного потока.
В результате приведенная стоимость денежных потоков (NPV) для проекта А равна 788,2 доллара. Расчет NPV для проекта А можно так же представить в виде таблицы и в виде шкалы времени:
 Точно таким же образом рассчитывается NPV для проекта Б.
Точно таким же образом рассчитывается NPV для проекта Б.
Поскольку коэффициенты дисконтирования уменьшаются с течением времени, вклад в приведенную стоимость проекта больших (4,000 и 6,000), но отдалённых по времени (третий и четвертый годы) денежных потоков будет меньше, чем вклад от денежных поступлений в первые годы проекта. Поэтому ожидаемо, что для проекта Б чистая приведенная стоимость денежных потоков будет меньше, чем для Проекта А.
У меня получилось, что NPV Проекта Б — 491,5 доллара.
Расчет NPV для проекта Б можно посмотреть в таблице и на рисунке со шкалой времени.
 Вывод: оба проекта можно принять, так как NPV обоих проектов больше нуля, а, значит, осуществление этих проектов приведет к увеличению стоимости компании-инвестора.
Вывод: оба проекта можно принять, так как NPV обоих проектов больше нуля, а, значит, осуществление этих проектов приведет к увеличению стоимости компании-инвестора.
Если эти проекты взаимоисключающие, то есть необходимо выбрать один из них, то предпочтительнее выглядит Проект А, поскольку его NPV заметно больше 788,2, чем NPV Проекта Б 491,5.
Цифры для расчета NPV инвестиционного проекта — в чём сложность?
Применить математическую формулу несложно, если известны все переменные. Когда у вас есть все цифры — денежные потоки и стоимость капитала — то вы легко сможете подставить их в формулу и рассчитать NPV. Но не всё так просто. Реальная жизнь отличается от чистой математики тем, что невозможно точно определить величину переменных, которые входят в эту формулу. Собственно говоря, именно поэтому на практике примеров неудачных инвестиционных решений гораздо больше, чем удачных.
а) Денежные потоки
Самый важный и самый трудный шаг в анализе инвестиционных проектов — это оценка всех денежных потоков, связанных с проектом. Во-первых, это величина первоначальной инвестиции (оттока средств) сегодня. Во-вторых, это величины годовых притоков и оттоков денежных средств, которые ожидаются в последующие периоды.
Сделать точный прогноз всех расходов и доходов, связанных с большим комплексным проектом, невероятно трудно. Например, если инвестиционный проект связан с выпуском на рынок нового товара, то для расчета NPV необходимо будет сделать прогноз будущих продаж товара в штуках, и оценить цену продажи за единицу товара. Эти прогнозы основываются на оценке общего состояния экономики, эластичности спроса (зависимости уровня спроса от цены товара), потенциального эффекта от рекламы, предпочтений потребителей, а также реакции конкурентов на выход нового продукта.
Кроме того, необходимо будет сделать прогноз операционных расходов (платежей), а для этого оценить будущие цены на сырье, зарплату работников, коммунальные услуги, изменения ставок аренды, тенденции в изменении курсов валют, если какое-то сырье можно приобрести только за границей и так далее. И все эти оценки нужно сделать на несколько лет вперед.
б) Ставка дисконтирования
Ставка дисконтирования в формуле расчета NPV — это стоимость капитала (cost of capital) для инвестора. Другими словами, это ставка процента, по которой компания-инвестор может привлечь финансовые ресурсы.
В общем случае компания может получить финансирование из трех источников:
- взять в долг (обычно у банка)
- продать свои акции
- использовать внутренние ресурсы (нераспределенную прибыль)
ЧИТАЙТЕ ТАКЖЕ: Ставка дисконтирования для инвестиционного проекта. Это WACC — средневзвешенная стоимость капитала
Финансовые ресурсы, которые могут быть получены из этих трех источников, имеют свою стоимость. И она разная! Наиболее понятна стоимость долговых обязательств (пункт 1 списка). Это либо процент по долгосрочным кредитам, который требуют банки, либо процент по долгосрочным облигациям, если компания может выпустить свои долговые инструменты на финансовом рынке. Оценить стоимость финансирования из двух остальных источников сложнее. Финансистами давно разработаны несколько моделей для такой оценки, среди них небезызвестный CAPM (Capital Asset Pricing Model). Но есть и другие подходы.
Стоимость капитала для компании (и, следовательно, ставка дисконтирования в формуле NPV) будет средневзвешенная величина процентных ставок их этих трех источников. В англоязычной финансовой литературе это обозначается как WACC — сокращение по первым буквам английской фразы Weighted Average Cost of Capital, что переводится как средневзвешенная стоимость капитала.
Зависимость NPV проекта от ставки дисконтирования
Понятно, что получить абсолютно точные величины всех денежных потоков проекта и точно определить стоимость капитала, т.е. ставку дисконтирования невозможно. В этой связи интересно проанализировать зависимость NPV от этих величин. У каждого проекта она будет разная. Наиболее часто делается анализ чувствительности показателя NPV от стоимости капитала.
Давайте рассчитаем NPV по проектам А и Б для разных ставок дисконтирования. Я сделала этот расчет в Excele, результаты приведены в таблице ниже:

Табличная форма уступает графической по информативности, поэтому гораздо интереснее посмотреть результаты на графике (нажать, чтобы увеличить изображение):

Из графика видно, что NPV проекта А превышает NPV проекта Б при ставке дисконтирования более 7% (точнее 7,2%). Это означает, что ошибка в оценке стоимости капитала для компании-инвестора может привести к ошибочному решению в плане того, какой проект из двух следует выбрать.
Кроме того, из графика также видно, что Проект Б (красная линия) является более чувствительным в отношении ставки дисконтирования. То есть NPV проекта Б уменьшается ,быстрее по мере роста этой ставки (красный график более крутой). И это легко объяснимо. В проекте Б денежные поступления в первые годы проекта невелики, со временем они увеличиваются. Но коэффициенты дисконтирования для более отдаленных периодов времени уменьшаются очень значительно. Поэтому вклад больших денежных потоков в чистую приведенную стоимость так же резко падает.
Например, можно рассчитать, чему будут равны 10,000 долларов через 1 год, 4 года и 10 лет при ставках дисконтирования 5% и 10%, то наглядно можно увидеть, как сильно зависит приведенная стоимость денежного потока от времени его возникновения:
В последнем столбце таблицы видно, что один и тот же денежный поток (10,000) при разных ставках дисконтирования отличается через год всего на 4.5%. Тогда как тот же самый по величине денежный поток, только через 10 лет от сегодняшнего дня при дисконтировании по ставке 10% будет на 37,2% меньше, чем его же приведенная стоимость при ставке дисконтирования 5%. Высокая стоимость капитала (=ставка дисконтирования) «съедает» существенную часть дохода от инвестиционного проекта в отдаленные годовые периоды, и с этим ничего не поделать. Это математика.
Именно поэтому, при оценке инвестиционных проектов денежные потоки, отстоящие от сегодняшнего дня более, чем на 10 лет, обычно не используются. Помимо существенного влияния дисконтирования, еще и точность оценки отдаленных по времени денежных потоков существенно ниже.
История с выбором между двумя проектами А и Б будет продолжена в следующих публикациях на тему методов оценки инвестиционных проектов. К сожалению, большинство статей в Интернете на эту тему написано сухо и коротко, и многие из публикаций содержат ошибки, что недопустимо.
Расчет NPV — пример в Excel
В нашем компьютерном веке стало гораздо проще делать любые расчеты. В программе Excel есть функция, с помощью которой расчет NPV можно сделать быстрее, чем по таблицам. И не нужно дисконтировать каждый поток вручную. Проще зайти в раздел Excel Формулы —> Финансовые и выбрать функцию ЧПС.
Пример расчета NPV для проекта А показан ниже:
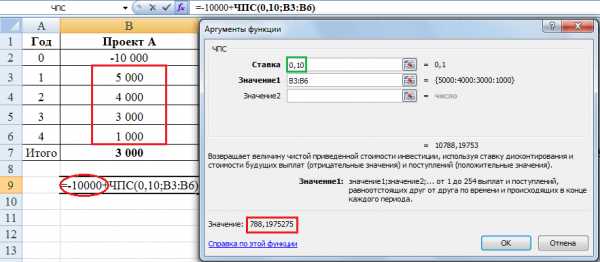
Единственная сложность заключается в том, что эта функция дисконтирует все потоки, которые вы выберете. Если же первый поток, как в проектах А и Б рассмотренных выше, приходится на период времени ноль, то его не надо вводить в ячейку значения. Первоначальная инвестиция в сумме -10,000 нужно добавить к тому значению, которое рассчитает функцию ЧПС. В этом примере дисконтируются ячейки B3-B6 (обведено красным в таблице), по ставке 0,10 (зеленый квадратик), приведенная стоимость получается равной 10,788.2. Если вычесть из этой суммы инвестицию 10,000, то получится NPV, равная 788,2. При расчете вручную мы получили 788,4, разница 0,2 получилась в результате округлений.
Другая функция программы Excel, расположенная в том же разделе финансовых формул, ЧИСТНЗ тоже считает приведенную стоимость денежных потоков, но она может это делать для неравных промежутков времени между потоками. В ней есть дополнительная ячейка, куда можно ввести диапазон дат, соответствующих времени поступления денежных средств.
И будет вам счастье и приличный счёт в банке.
Финансовая грамотность необходима каждому человеку. Современная экономика — это сложный механизм перекачивания денег из одного кармана в другой. И нужно не только научиться зарабатывать деньги, но и вкладывать их.
Учиться быть инвесторами желательно еще до того, как у вас появятся деньги. Если в будущем вам повезет, и вы выиграете миллион долларов в лотерею, то вы должны быть готовы к этому. Если вам удастся заработать достаточные для инвестирования средства, то тем более захочется распорядиться ими так, чтобы приумножить.
Другие статьи на этом сайте из рубрики «Финансы»:
Вернуться на главную страницу
msfo-dipifr.ru